Tobler地理學第一定律:all attribute values on a geographic surface are related to each other, but closer values are more strongly related than are more distant ones.
空間自相關指的是空間單元的數據與其周遭空間單元的相似性,
今天我們以Pysal的說明頁面(ESDA with PySAL)為主軸,一步步進行與空間自相關相關的測試
大綱:
最簡單的spatial weight可以距離相關為weight
以外,可以進一步用相鄰性計算spatial weight,常見包含Rook、Queen、Bishop等相鄰性
請參考Pysal
還有其他如核密度權重等等
在計算之前,需要一些前處理
我們在第九天處理一個行政區路燈統計
今天進一步計算路燈永和區的路燈分佈密度(以里為單元)
看看是否有哪幾區特別亮:
import geopandas as gpd
light=gpd.read_file('output/light.shp',encoding='utf-8')
light=light[light.is_valid]
light=light[light['district']=='永和區']
light.crs = {'init' :'epsg:3826'}
light=light.reset_index()
village=gpd.read_file('data/village/village.shp',encoding='utf-8')
village=village[village.is_valid]
village=village[village['ADMIT']=='永和區']
village.crs = {'init' :'epsg:3826'}
village=village.reset_index()
result=gpd.tools.sjoin(light[['geometry','district']], village[['ADMIV','ADMIT','geometry']], op='within',how="right")
result['count']=1
result=result.dissolve(by='ADMIV', aggfunc='sum')
result['avg']=result['count']/result.area
result
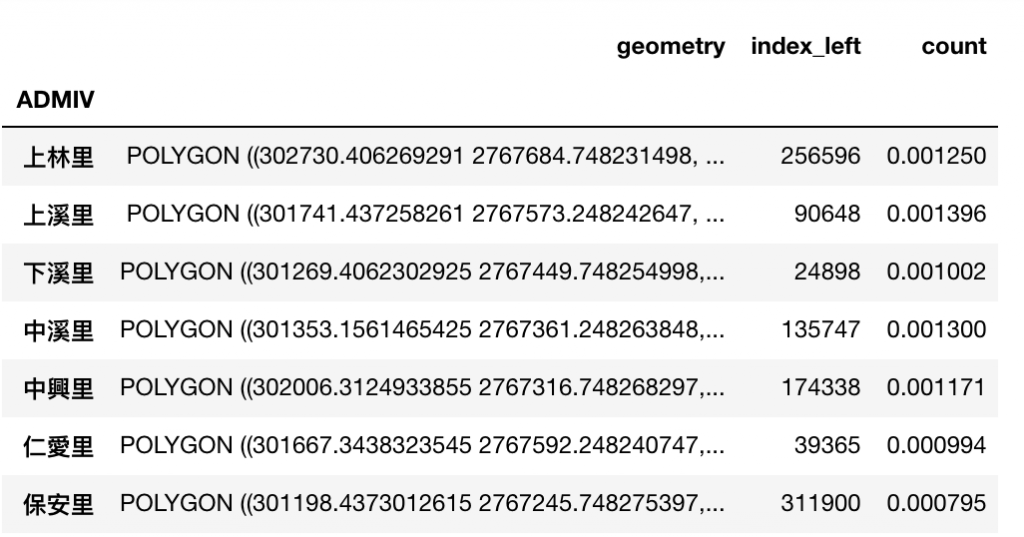
經過以上計算,路燈密度欄位為count
使用Pysal將count分成五個量級,並繪圖展示:
cl = pysal.Quantiles(result['count'], k=5)
result.assign(cl=cl.yb).plot('cl', legend=True, categorical=True)
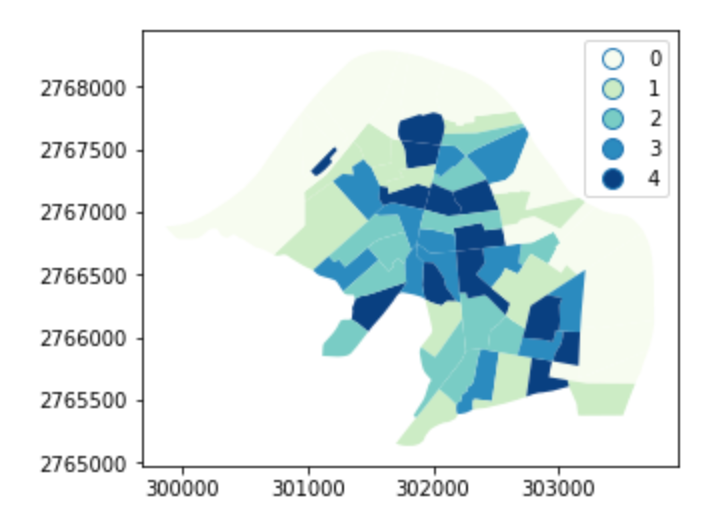
以上成果是原始的面量圖呈現
以下我們用Pysal計算spatial weight,採用Queen的相鄰性
如果要使用GeoDataFrame的話,可以透過libpysal
wq = libpysal.weights.Queen.from_dataframe(result)
wq.transform = 'r' # row standardization
有了spatial Weight,可以計算spatial lag空間間隔
y = result['count']
ylag = libpysal.weights.lag_spatial(wq, y)
一樣分成五個等級繪圖
cl = pysal.Quantiles(ylag, k=5)
result.assign(cl=cl.yb).plot('cl', legend=True, cmap='GnBu', categorical=True)
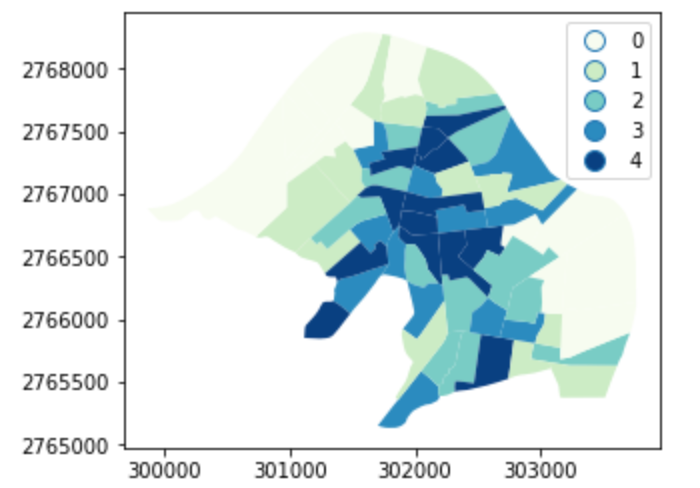
注意:不同的spatial weight會產生完全不同的結果,邦友可以自行測試
spatial lag的結果,我們以散布圖與原本的值比較(Moran Scatterplot)
看看是否合理
import numpy as np
import matplotlib.pyplot as plt
y = result['count']
b, a = np.polyfit(y, ylag, 1)
f, ax = plt.subplots(1, figsize=(9, 9))
plt.plot(y, ylag, '.', color='firebrick')
plt.vlines(y.mean(), ylag.min(), ylag.max(), linestyle='--')
plt.hlines(ylag.mean(), y.min(), y.max(), linestyle='--')
plt.plot(y, a + b*y, 'r')
plt.title('Moran Scatterplot')
plt.ylabel('Spatial Lag of count')
plt.xlabel('count')
plt.show()
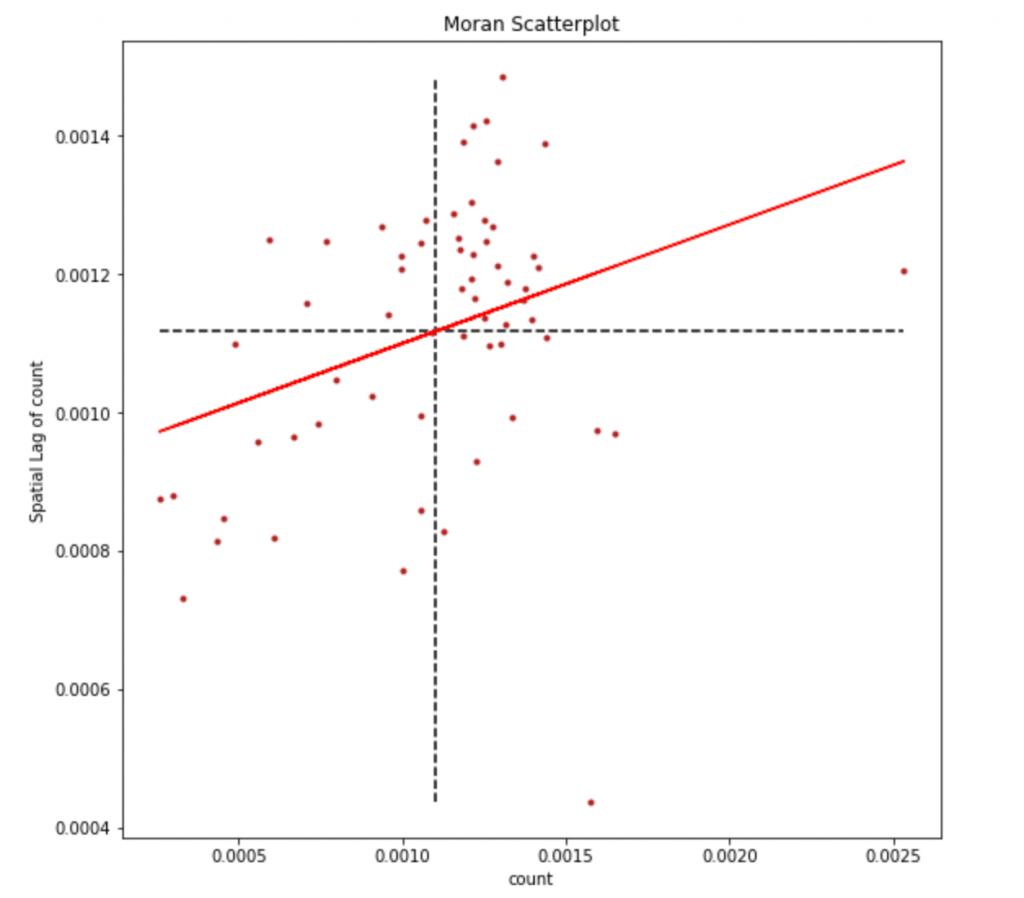
全域自相關的部分,在Python中可使用Pysal esda計算Moran's I全域空間自相關
Moran's I的公式說明詳見說明
import esda
mi = esda.moran.Moran(y, wq)
mi.I
結果:0.171730
全域Moran’s I的值在-1至1,接近1表示資料正相關,也就是有群聚性,接近-1則是越顯分散
此外,越接近0表示自相關程度不高(越不顯著)
注意:不同的spatial weight會產生完全不同的結果,邦友可以自行測試
從上面的成果看來,可知永和區的路燈密,在空間上具有不明顯的群聚的現象
(有偏袒,沒有特別偏袒)
接下來使用esda計算Moran區域型的空間自相關
看看哪邊特別亮
li = esda.moran.Moran_Local(y, wq)
li.q
注意:不同的spatial weight會產生完全不同的結果,邦友可以自行測試
繪圖
result.assign(cl=li.q).plot('cl', legend=True, cmap='GnBu', categorical=True)
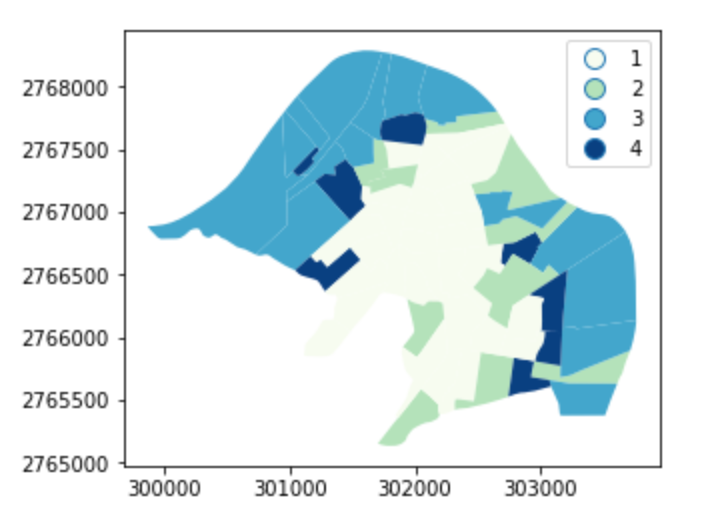
Local Moran’I會算出1-4個等級,
在區域型的空間自相關的計算中,會進行假設檢定的統計測試,以測試所算之值顯不顯著
在範例中,設定通過0.05顯著水準的P測試
sig = li.p_sim < 0.05
hotspot = 1 * (sig * li.q==1)
coldspot = 3 * (sig * li.q==3)
doughnut = 2 * (sig * li.q==2)
diamond = 4 * (sig * li.q==4)
spots = hotspot + coldspot + doughnut + diamond
spot_labels = [ '0 ns', '1 hot spot', '2 doughnut', '3 cold spot', '4 diamond']
labels = [spot_labels[i] for i in spots]
result.assign(cl=labels).plot('cl', legend=True, cmap='GnBu', categorical=True)
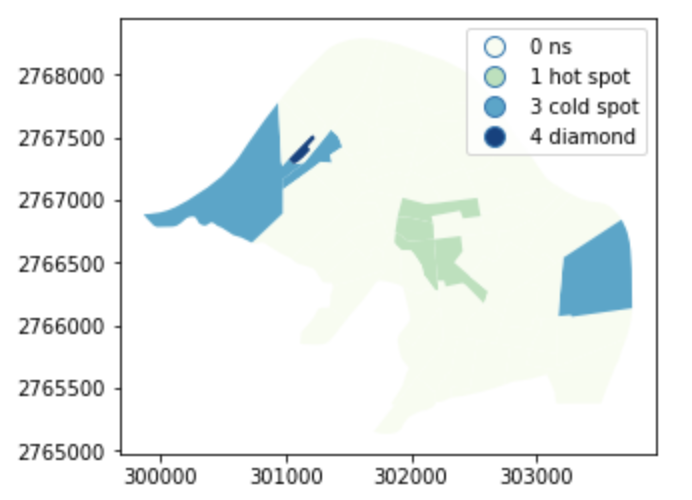
也可以獨立來看
hotspot:自相關高,正相關,通過設定的統計測試
也就是自己亮周遭也亮的區域
spots = ['n.sig.', 'hotspot']
labels = [spots[i] for i in hotspot*1]
result.assign(cl=labels).plot('cl', legend=True, cmap='GnBu', categorical=True)
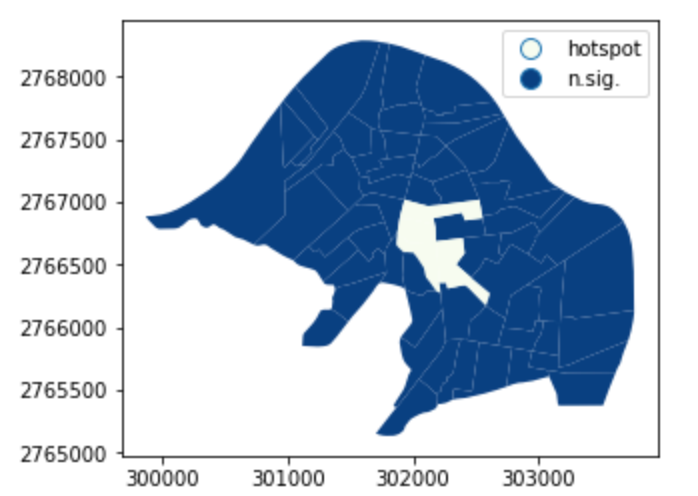
例如:所謂一支獨秀
spots = ['n.sig.', 'diamond']
labels = [spots[i] for i in diamond*1]
result.assign(cl=labels).plot('cl', legend=True, cmap='GnBu', categorical=True)
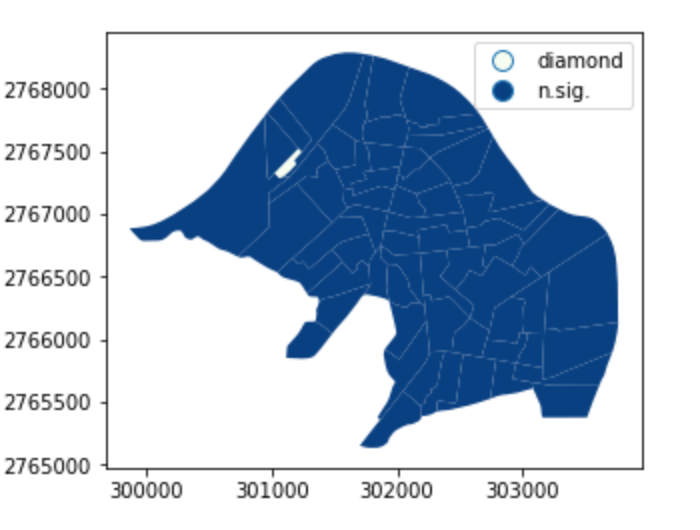
由於空間自相關的公式較多,在此篇幅無法一一表達清楚,僅能針對操作稍做測試
相關細節歡迎邦友參考:
地理論壇 Geogforum - GEOGDAILY.地理眼
Global Moran's I| ArcGIS for Desktop
ESDA with PySAL
GitHub - pysal/esda: statistics and classes for exploratory spatial data analysis
